4.2 Zpracování a analýza dat
Pro odvození závislostí ve složité kritické infrastruktuře, v případě použití, tj. infrastruktura metra, je v předložené práci použita teorie citlivostí, kterou lze ocenit sílu jednotlivých závislostí, tj. míru jejich zranitelnosti, což znamená schopnosti závislostí způsobit selhání (KI, metra). Matice jsou pro jejich následnou analýzu transformované do grafu.
4.2.1 Teorie citlivosti
Z důvodů lepší interpretace a práce s informačními systémy lze zranitelnost definovat také jako citlivost s využitím teorie citlivostí [87,88], kterou lze poptat následujícím vztahem [89]:
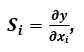
(22)
kde Si je absolutní citlivost výstupní funkce y na parametr vstupní funkce xi. Přičemž dle zdroje [90] je ve smyslu elektronických systémů y = f(x1,..,,xi,…,xN) síťovou (resp. systémovou) funkcí, jež je závislá na obvodovém parametru xi. Změna výstupní funkce systému je tedy závislá na její citlivosti a na změně vstupních parametrů xi, uvedený vztah se z praktických důvodů zapisuje v maticovém tvaru, tj. pomocí matice citlivostí S [90]:
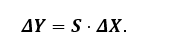
(23)
U elektrických, elektronických a programovatelných elektronických systémů (dále jen E/E/PE) je výhodné počítat s relativní citlivostí a s relativní změnou parametru, protože umožňuje výpočet tolerancí výstupní veličiny, návrhu tolerancí vstupních parametrů, optimalizaci citlivosti elektrického obvodu, hledání nejcitlivějších prvků, tj. prvků s největším vlivem na změny výstupní veličiny [90].
Pro práci s aktivy je vhodné pracovat s citlivostí absolutní, protože ačkoliv jsou dané stupnice pro hodnocení kritičností normalizované, každá funkce aktiva má jiný fyzikální základ.
4.2.2 Maticový zápis a kodifikace názvů
Zvyklost praxe je uvádět vztahy jednotlivých prvků v tabulkách. V našem případě se jedná o citlivost, tedy vztah vstupních veličin (pohromy, resp. aktiva a výstupních veličin (funkce systému, resp. aktiv):
Pro lepší přehlednost je použit maticový zápis znázorněn tabulkou 8.
Tabulka 8 Formát tabulky kritičností aktiv pro jednotlivé pohromy.
| Pohroma 1 | . … | Pohroma n | |
| Aktivum 1 | S11 | . … | Sn1 |
| … | . | . … | . |
| Aktivum m | S1m | . … | Snm |
Tabulku 8 převedeme do maticového tvaru, ve které yi označuje aktiva a xi označuje pohromy. Maticový zápis umožňuje provádět patřičné operace a převod matice do grafu pro analýzu scénářů.
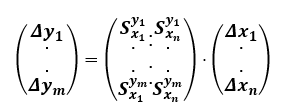
(24)
Vstupní parametry xi mohou ve skutečnosti představovat také výstupní parametry jiných aktiv (funkcí). V případě, že chceme zobrazit souvislosti více do hloubky, lze kombinací vstupních a výstupních parametrů na obou stranách rovnice vytvořit zřetězení, tj. pro účely práce „zřetězené matice citlivostí“, které v technice znamenají míru zranitelností závislé na míře propojení veličin nebo parametrů [6,33].
V praxi uvedené tabulky a matice mohou nabývat velkých rozměrů a pro zajištění jejich čitelnosti je vhodné zavést přiměřenou kodifikaci názvů. V disertační práci je použito číselné označení pohrom uvedené v příloze B. Použité označení skupin aktiv je uvedeno v Tabulce 9.
Tabulka 9 Použité označení skupin aktiv.
| Skupina | Označení |
| Konstrukce | AK |
| Technika | AT |
| Personál | AP |
| Místa | AM |
| Funkce | AF |
| Vazby a toky | AV |
| Organizace a ekonomika | AO |
Číselné označení dílčích tříd aktiv použitých níže v disertační práci je z důvodu jejich velkého rozsahu uvedeno v příloze C.
4.2.3 Transformace matic do grafu
Využitím teorie grafů, popsané např. v práci [91], můžeme zranitelnosti zobrazit pomocí ohodnoceného orientovaného grafu. Pro vytvoření grafu je třeba:
- použít matice citlivostí, uvedené v předchozích odstavcích 4.2.1 a 4.2.2,
- transformovat matice citlivosti do matic sousedností, které vyjadřují míry těsnosti propojení sledovaných veličin. Předmětné matice jsou základem pro generování grafů, které vyjadřují míry propojení příslušných veličin.
Pro vytvoření matic sousedností je použit nástroj MS Excel, export souboru s maticemi je dále importován do nástroje určeného pro práci s grafy – Gephi 1Zpracování a analýza dat, nástroj: G2ephi – The Open Graph Viz Platform verze 9.0.2 [92].
Proces transformace do grafu lze rozdělit do následujících kroků:
- Sestavení matic sousedností (měr těsnosti propojení) z matic citlivostí (měr zranitelností).
- Sestavení orientovaného grafu – grafická interpretace.
- Ohodnocení hran (zranitelnost dané vazby – propojení) a uzlů (zranitelnost, resp. kritičnost sledovaných veličin, aktiv).
- Analýza grafu a grafická interpretace výsledků.
4.2.3.1 Sestavení matic sousedností z matic citlivostí
Matice sousedností [91] vyjadřuje relace mezi dvěma objekty (v uvedeném případě vstupních a výstupních parametrů funkce, respektive mezi uzly, které reprezentují aktiva či pohromy). Jejich sloupce i řádky vyjadřují tutéž množinu objektů ve stejné posloupnosti. Aby bylo možno použít matice citlivostí, je nutné začít se vstupními parametry funkce a následně pak s výstupními parametry funkce takto: APdii02; ATv; Atzb; AVi06 (použitá označení jsou vysvětlená v příloze C).
Podle teorie matic postupujeme tak, že do prázdné matice sousedností dosadíme transponovanou matici citlivostí a za předpokladu, že jde o podklad pro konstrukci orientovaného grafu, ve kterém vztahy jsou jednosměrné, do ostatních pozic matice doplníme nuly „0“. Tabulka 10 reprezentuje výslednou matice sousedností, modře podbarvené buňky tabulky znázorňují transponovanou matici citlivostí.
Tabulka 10 Matice sousedností pro vztah (44) (odstavec 6.1.3).
| APdii02 | ATv | ATzb | AVi06 | |
| APdii02 | 0 | 0 | 0 | 1 |
| ATv | 0 | 0 | 0 | 1 |
| ATzb | 0 | 0 | 0 | 1 |
| AVi06 | 0 | 0 | 0 | 0 |
Předmětný algoritmus lze aplikovat pro všechny předchozí jednoduché vztahy, ve kterých nejsou některé vstupní a výstupní parametry společné. Pro zřetězené matice je nutné brát v potaz právě společné vstupní a výstupní parametry a vytvářet posloupnost uzlů obezřetně. Zápis zřetězené matice je uveden v tabulce 11
Tabulka 11 Matice sousedností pro zřetězené matice (vztah (45) a 6.1.3).
| AKs01 | AKk06 | ATv | AVi06 | ATe | AMtp03 | APdii02 | ATzb | AVm01 | |
| AKs01 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 |
| AKk06 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 |
| ATv | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 |
| AVi06 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 |
| ATe | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 |
| AMtp03 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 |
| APdii02 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| ATzb | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| AVm01 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
4.2.3.2 Sestavení orientovaného grafu – grafická interpretace
Orientovaný graf je dle definice [91] vyjádřen uspořádanou trojicí:
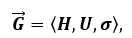
(25)
kde H je množina hran, U je množina uzlů a σ je incidenční relace vyjádřená vztahem:
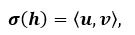
(26)
kde u je počáteční vrchol a v je koncový vrchol. Graf G lze plně odvodit z matic sousedností [91]. Graf pro tabulku 10 je na obrázku 13 a pro tabulku 11 je na obrázku 14.
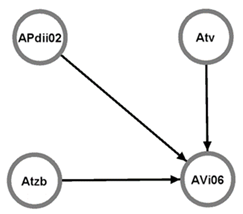
Obrázek 13. Graf pro tabulku 3 (AVi06), [3].
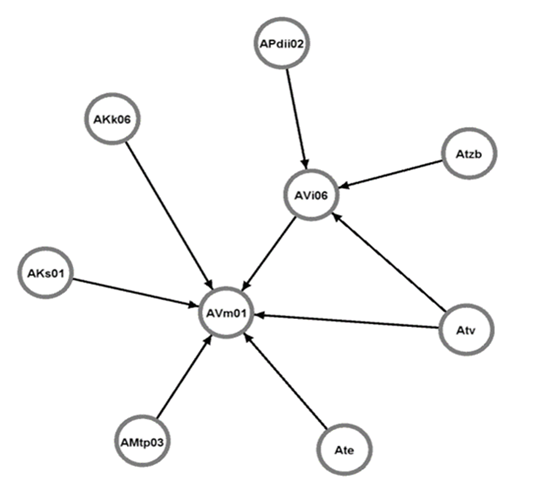
Obrázek 14. Graf pro tabulku 4 (Avi06-m01), [3].
4.2.3.3 Ohodnocení hran (zranitelnost dané vazby) a uzlů (zranitelnost, resp. kritičnost)
Obrázky 13 a 14 znázorňují grafy dle uvedených matic sousedností, ale nereprezentují ohodnocení hran a parametrů uzlů. Ke každé hraně a uzlu lze textem připsat požadované informace (ohodnocení pomocí váhy hrany, resp. zranitelnost či kritičnost uzlu). S využitím SW nástroje [92] lze navíc uvedené parametry různě interpretovat graficky, tj. změna velikosti či barvy hran a uzlů podle jejich vlastností.
Váha hrany je pro účely předložené práce ohodnocení mírou propojení čili mírou citlivosti (resp. zranitelnosti) cílové ho aktiva na vstupní parametr (funkce aktiva či pohroma).
Textové ohodnocení uzlů v disertační práci znázorňuje kritičnost, pokud je pro danou analýzu potřeba (např. Obrázek 21 v odstavci 6.2.3).
Rozměry a barvy uzlů a hran použité v disertační práci jsou popsané v následujícím odstavci.
4.2.3.4 Analýza grafu a grafická interpretace výsledků
Pro zobrazení grafu byl použit nástroj Gephi 0.9.2 [92]. Výchozí zobrazení (rozmístění) uzlů na ploše v nástroji není ideální, proto je nutné rozložení vhodně upravit. Lze využít manuálního rozmisťování uzlů podle potřeby a typu uzlu nebo je také možnost využít známých algoritmů. Zároveň barevné rozlišení uzlů a hran a jejich velikost je vhodné upravit podle jejich stupně, vah a dalších parametrů.
Pro analýzu grafů bylo zvoleno následující nastavení volitelných parametrů, které nástroj umožňuje [92]:
- Rozložení:
- silově zaměřené Fruchterman-Reingold [93],
- oblast: 10000; gravitace: 10; rychlost 1, které ovlivní výsledné rozložení uzlů a hran na pracovní ploše (resp. na plátně) v SW nástroji.
- Uzly:
- velikost dle „Stupně dovnitř“; min: 10; max: 50; exponenciálně, uvedené nastavení na pracovní ploše exponenciálně zvětší uzly, které mají více vstupujících hran,
- barva dle „Stupně dovnitř“; min: černá; max: červená; lineárně, uvedené nastavení na pracovní ploše červeně zabarví uzly, které mají více vstupujících hran,
- „stupeň dovnitř“ vyjadřuje počet vstupujících hran do daného uzlu bez ohledu na jejich váhu,
- „stupeň ven“ vyjadřuje počet vystupujících hran z daného uzlu bez ohledu na jejich váhu.
- Hrany:
- ve výchozím nastavení tloušťka dle váhy,
- barva dle „Váhy“; min: černá; max: červená; v intervalu mezi minimem a maximem lineárně rozložená.
